99클럽 코테 스터디 5일차 TIL - 컴퓨터에게 일을 다 시키지 말자

 

문제 - 점 찍기 문제링크

프로그래머스

오늘 배운 점

때로는 컴퓨터에게 일을 다 시키기보다 수학적 해법을 찾아봅니다.
더 빠른 풀이는 없는지 찾아봅니다.

 

문제 설명

제한 사항

입출력 예

k: 몇 배수로 점프할지를 나타냅니다. k = 2라면 0, 2, 4, 6, ... 이 됩니다.
d: 원점 기준 최대 허용 거리를 나타냅니다.

 

접근 과정

사실 문제에서 원이 주어지진 않았지만 원점으로부터 거리가 $d$가 넘는 지점에는 점을 찍지 않는다는 규칙이 있기 때문에 반지름을 $d$로 하는 원을 그렸습니다.

그림으로 표현하면 이렇게 볼 수 있습니다.

 
다시말해 $ xy $ 좌표계의 원점에서 반지름이 $ d $인 원을 그렸을 때, $ x $축, $ y $축, 원으로 둘러싸인 영역 내의 점 개수를 구하면 됩니다. 영역은 각 축과 원을 포함합니다. 이때, 점이 놓이는 규칙은 $ (0, 0) $에서 시작하여 $ x, y $좌표가 각각  $ k $의 배수만큼 증가하며 놓일 수 있습니다.
 
점은 해당 1사분면 영역 내에서만 배치될 수 있고 원으로 막혀 있기 때문에 원의 좌표를 이용해서 문제를 풀어야 합니다.
그래서 우선 $ 0\leq x\leqslant d $ 인 $ x $좌표에 대해 원의 $ y $값을 구한 후, 개별 $ x $에 대해 $ 0\leq k*i\leqslant y $를 만족하는 $ i $를 구했습니다. 위 부등식을 만족하는 $ i $를 구할 때, $ i $를 $ 0 $부터 $ 1 $씩 증가시켜가며 확인해가는 방식으로 풀 수 있고, $ O(d^{2}/k) $의 시간복잡도입니다.

import math
def solution(k, d):
    answer = 0
    
    # x좌표 이동
    for x in range(0, d + 1, k):
        # 원의 y값 구하기
        y = math.sqrt(d**2 - x**2)
        
        for i in range(int(y) + 1):
            if k * i <= y:
                answer += 1
            else:
                break
    return answer

 
 
결과는 시간초과가 납니다. 

시간초과

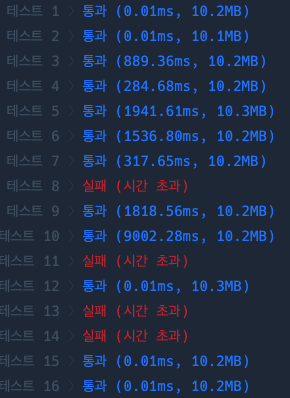
$ d $가 최대 100만이기 때문에 $ O(d^{2}/k) $로는 풀 수 없습니다.
$k$로 나눈 몫을 취하는 방식으로 푼다면 $ O(d/k) $인 풀이를 구현할 수 있습니다.

정답 코드 1 

import math
def solution(k, d):
    answer = 0
    
    # x좌표 이동
    for x in range(0, d + 1, k):
        # 원의 y값 구하기
        y = math.sqrt(d**2 - x**2)
        
        # k로 나눈 몫 + x축에 있는 점 1개 = 점 개수
        answer += y // k + 1
        
    return answer

 
$x$를 $0$에서부터 시작하여 $k$만큼 점프해 가며 원의 $y$좌표를 구한 후, $ y $를 $k$로 나눈 몫을 취하면 $0< i*k\leq y$인 $i$의 개수를 구할 수 있습니다. 여기에 $y = 0$인 경우를 추가해줘야 하니 $+ 1$을 해주었습니다. 

제출 결과 1

정답 코드 2

풀이를 마친 후 reduce를 사용해서 같은 문제를 풀어보았습니다.

import math
from functools import reduce

def solution(k, d):
    return reduce(lambda acc, x: acc + math.sqrt(d**2 - x**2) // k + 1,
                  range(0, d + 1, k),
                  0)

 

제출 결과 2

 

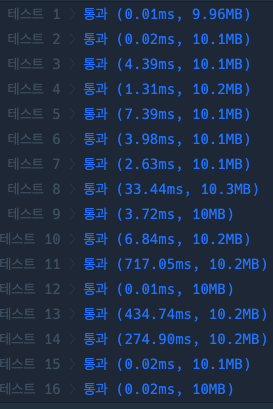
정답 코드 3

sum으로도 풀어보았습니다.

import math

def solution(k, d):
    return sum([1 + math.floor(math.sqrt(d ** 2 - x ** 2)) // k
    for x in range(0, d + 1, k)])

 

제출 결과 3

 

총평

사람이 최적화 해줄 수 있는건 최적화 해주는게 좋습니다.
for문, reduce, sum 방식 간에 시간 차이는 유의미하지 않았습니다.
reduce는 sum, min, max, all, any같은 pythonic tool들로 대체되었다고 합니다.(참고자료)