레드-블랙 트리 Red-Black Tree 5가지 조건의 의미

레드 블랙 트리의 포함관계

포함관계: 트리 > 이진 트리 > 이진 탐색 트리 > 균형 이진 트리 > 레드블랙 트리

 

1. 트리

 

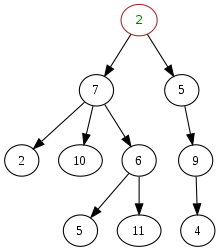
그림1. 트리 구조

 

트리 구조는 일반적으로 위의 그림처럼 생겼다.

트리 구조를 트리라고 부르는 이유는 나무의 뿌리와 비슷하게 생겼기 때문이다.

나무 뿌리

위의 나무 그림에서 뿌리가 시작되는 지점이 첫번째 그림에서의 2번 동그라미고,

뿌리로부터 뻗어나가는 곁뿌리들이 2번에서부터 밑으로 선으로 연결되어 있는 동그라미들이다.

 

여기서 동그라미는 전문용어로 노드(node)라고 불리고, 선은 간선(edge)이라고 불린다.

 

2번 노드는 뿌리의 시작점이라서 뿌리를 뜻하는 root를 사용해서 루트(root)노드라고 불린다.

 

자기랑 간선 하나로 연결되어 있는 노드가 밑에 있으면 자식노드, 위에 있으면 부모 노드라고 부른다. 

 

자식이 없는 노드를 리프(leaf, 잎)노드라고 부른다.

 

루트노드에서 임의의 리프노드들 까지 가는 모든 경로 중에서 가장 길이가 긴 값이 트리의 높이이다.

 

2. 이진 트리

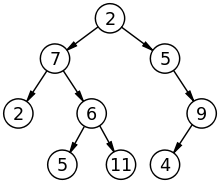
그림3. 이진트리

그림1의 트리를 보면, 7번 노드의 자식은 2, 10, 6번 노드로 총 3개의 노드를 자식노드로 가지는 것을 확인할 수 있다.

여기서 이진(binary) 트리란, 노드의 자식을 최대 2개까지만 가질 수 있는 트리를 의미한다.

그림3의 이진트리는 잘 보면 각 노드의 자식 수는 0개, 1개, 최대 2개를 가지고, 3개 이상을 가지는 노드는 없는 것을 확인할 수 있다.

 

3. 이진 탐색 트리

이진 탐색 트리는 우선, 정보를 저장하는 저장소로 이진 트리를 이용해서 각 노드에 저장할 정보를 각각 넣는다. 이진 트리와 다른 점은, 어떠한 규칙을 준수하면서 저장된다는 것이다. 먼저, 각 노드는 자신을 식별할 수 있는 키(key)값을 가지고 있을 때,

 

규칙: 자신의 왼쪽 자식은 자신보다 작은 키값을 가지는 노드여야 하고, 오른쪽 자식은 자신보다 큰 키값을 가지는 노드이어야 한다.

 

이후, 특정 키값을 가지는 노드 정보가 필요할 때 루트 노드부터 확인해가면서 내가 찾는게 맞나 다른가를 보고, 맞으면 해당 노드에 들어 있는 정보를 받고, 다르면 해당 노드의 왼쪽 자식을 확인하러 갈지, 오른쪽 자식을 확인하러 갈지 판단해서 이동한다. 판단 기준은 현재 노드보다 키값이 작으면 왼쪽 자식으로, 크면 오른쪽 자식으로 간다. 이렇게 하면, 한번 판단해서 왼쪽 혹은 오른쪽으로 갈 때마다 다른쪽의 모든 노드는 확인할 필요가 없어지기 때문에 확인해야 할 노드가 1/2배씩 줄어든다. 따라서 노드가 총 N개라면, 1/2배씩 줄여 나가다가 1개가 남는 순간 내려가는게 끝난다.

 

식을 세워보면, N/(2^h) = 1이고, h = log_2(N)이 된다. h의 뜻은 h번만큼 내려가면 노드가 1개인 때까지 도달할 수 있다는 것이다. 그래서 결국 탐색의 시간복잡도 = O(logN)이다.

 

4. 균형 이진 탐색 트리

균형 이진 트리는 이진 탐색 트리에 '균형'이라는 접두사가 붙었다. 균형을 이루는 이진 탐색 트리라는 뜻인데, 그렇다면 기존에는 균형을 이루고 있지 못한다는 소리다. 이게 무슨 소리일까.

 

일단 이진 탐색 트리에 10, 20, 30, 40, 50을 넣어보자.

이진탐색트리

결과를 보면 10->20->30->40->50 이렇게 일렬로 오른쪽 자식만을 가지는 트리가 만들어진다. 이때, 루트노드의 왼쪽 경로는 (10)인데 오른쪽 경로는 (10->20->30->40->50)으로 두 경로 길이가 각각 0과 4가 된다. 결과적으로 이 트리의 높이는 4가 된다. 이후 50을 찾고 싶다면 총 5번 내가 찾고 있는 노드가 맞는지 확인해야 한다. 이는 최악의 경우로, 기존에 탐색의 시간복잡도였던 O(logN)이 무색하게 N = 5를 대입해보면 log5이고, 실제 연산횟수인 5보다 훨씬 작게 계산되는걸 확인할 수 있다. 따라서 항상 O(logN)을 보장하지는 않게 된다.

 

균형 이진탐색 트리는 트리의 높이를 최저로 만들어주는 트리다. 트리의 높이를 최저로 만들어주기 위해서는 노드들을 최대한 꽉꽉 루트노드부터 양쪽 자식에 채워넣어가면서 밑으로 안 뻗어나오게 트리를 만들어줘야 한다. 이렇게 트리 높이를 최저로 만들어주면, 루트에서 시작해서 임의의 리프노드까지의 경로의 길이가 서로 비슷해지게 된다. 이 비슷해지는 것을 균형을 맞춘다고 표현한다. 결론은 모든 루트노드-리프노드까지의 거리를 최대한 같게 유지해주는게 균형 이진탐색 트리다.

 

저 트리가 레드블랙 트리였다면 같은 순서로 트리에 넣을 시 이런 모양이 된다.

 

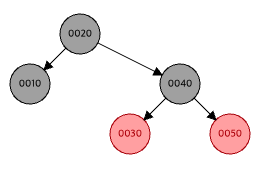
레드블랙 트리에 넣은 결과

트리의 높이가 2이 되면서 트리의 높이가 기존의 4에서 2로 대폭 감소했다. 이렇게 되면 이후 50을 찾아야 할 경우 이진탐색트리는 10->20->30->40->50까지 총 5번 확인을 해야하지만, 레드블랙트리의 경우 20->40->50 이렇게 3번만 확인하면 찾을 수 있어서 더 빨리 50을 찾는다. 50의 의미는 이 노드의 key=50이라는거고, key=50인 노드를 찾아서 이제 내용을 수정, 삭제하는 등 우리가 원하는 작업을 수행할 수 있다.

 

5. 레드 블랙 트리

레드블랙트리

이진탐색트리를 균형있게 만들어주는 기법에는 여러 가지가 있다. 그중 하나가 바로 레드 블랙 트리다.

레드 블랙 트리는 기본적으로 삽입과 삭제는 기존의 이진탐색트리와 똑같다.

 

다른점

1. 각 노드는 색을 가지고, 이는 레드와 블랙이다.

- 이해하기 쉽게 레드와 블랙으로 만든거지, 실제로 코드 작성시에는 0과 1나 -1,1같이 구별할 수 있는 두 값이면 된다.

 

2. 각 노드는 자신의 부모 노드를 알고 있다. 기존의 이진 탐색트리는 양쪽 자식 노드만 알지 부모노드는 알지 못했다(접근할 수 없었다)

 

3. NIL 노드라는 개념이 도입된다. NIL 노드는 아무 값도 없다는 뜻의 NULL과 비슷한데, 대상이 노드일 뿐이다. 따라서 NIL노드는 아무값도 없는 노드를 의미한다. 기존의 이진탐색 트리는 자식이 없으면 없는대로 뒀었는데(NULL), 레드 블랙 트리는 자식이 없으면 그 자리에 NIL 노드를 넣는다. 또한, 모든 노드가 하나의 NIL노드를 공유해서 자신의 자식으로 사용하는게 일반적이다.  

 

우선 이렇게 세팅을 한 후, 아래 6가지 조건을 만족해야 한다.

조건 0. 기존 이진탐색 트리 규칙은 만족해야 한다.

조건 1. 모든 노드의 색은 레드이거나 블랙이다.

조건 2. 루트 노드의 색은 블랙이어야 한다.

조건 3. NIL노드는 블랙이다.(모든 리프 노드들(NIL)은 블랙이다)

조건 4. 레드 노드에는 레드 자식이 없다.(=레드 노드의 자식노드 양쪽은 모두 블랙이다(NIL노드가 있기 때문)=레드 노드는 연달아 올 수 없다)

조건 5. 특정 노드에서 하위 NIL노드에 도달하는 모든 경로에는 같은 개수의 블랙노드가 있다(NIL노드는 제외)

전제: 새로 추가될 노드의 색은 레드이다.

 

 

---

레드블랙 트리에서 새롭게 추가되는 조건들

 

조건 1. 모든 노드의 색은 레드이거나 블랙이다.

- 레드블랙트리 기법은 노드에 색을 칠하고, 이 색을 이용해서 트리의 균형을 맞춘다.

 

조건2. 루트 노드의 색은 블랙이어야 한다.

- 루트 노드가 블랙이나 레드로 고정되어 있지 않으면, 우선 비어 있는 트리에 새 노드를 넣을 때 루트노드를 어떤 색으로 할지 명확하지 않아서 일단 색을 고정해야 하고, 블랙 대신 레드로 고정한다면 다음과 같은 플로우가 발생한다.

 

1. 빈 레드-블랙 트리를 만들고 루트 노드가 될 첫 번째 노드를 추가한다.
2. 루트 노드는 레드이 된다.
3. 루트 노드의 양 자식에 NIL 노드가 붙고, 색은 블랙이다.
4. 이제 두 번째 노드를 추가하면 루트의 자식이 되고(왼쪽 자식이라고 가정) 레드 노드(루트)는 빨간색 자식을 가질 수 없기 때문에 루트노드의 왼쪽 자식은 블랙이 된다.
5. 그러나 이는 루트에서 모든 리프까지의 블랙 노드 수가 동일해야 한다는 규칙을 깨뜨린다.(루트노드의 왼쪽경로: 검은색 2개 오른쪽 경로: 검은색 1개)
   
6. 이 문제를 해결하기 위해 루트(레드)와 왼쪽 자식(블랙)의 색을 서로 교체한다.
7. 루트(블랙)가 빨간색이 아니므로 루트가 레드인 전제조건이 깨진다.
8. 따라서 루트노드는 블랙이어야 한다.

조건 3. NIL노드는 블랙이다.(모든 리프 노드들(NIL)은 블랙이다)

- 조건4에서 레드노드는 레드 자식을 가지지 않아야 하고, 레드노드도 자식이 없을 때 NIL노드를 자식으로 가지므로, NIL노드는 블랙이어야 한다.

 

(참고: NIL노드가 필요한 이유?: 자식이 없을 때 자식 자리에 NIL 노드 대신 NULL이 들어가면, 자식의 색을 파악하기 전에 우선 자식이 있는지 없는지 판단하기 위해 NULL체크를 하고 나서 NULL이 아닐 경우 자식의 색에 접근할 수 있다. 하지만 NULL 대신  NIL노드를 넣으면 NULL체크 필요없이 바로 자식에게 접근할 수 있다. 또한, 노드 삭제 이후 균형을 이루는 재조정 작업에서 NIL노드가 필요하다.)

 

조건 4. 레드 노드에는 레드 자식이 없다.(=레드 노드의 자식노드 양쪽은 모두 블랙이다=레드 노드는 연달아 올 수 없다)

- 레드노드의 자식으로 레드노드가 붙을 수 있게 된다면, 조건5를 만족하는 상태에서 계속 레드노드의 자식에 레드노드가 붙을 수 있게 되면서 모든 조건을 만족하면서도 계속 높이 균형은 깨지게 된다. 따라서 레드 노드에는 레드 자식이 오면 안된다.

 

조건 5. 특정 노드에서 하위 NIL노드에 도달하는 모든 경로에는 같은 개수의 블랙노드가 있다(NIL노드는 제외)

- 예를 들어보자면, 경로의 블랙개수가 3일 때, 모든 경로의 블랙노드 개수가 같아야 된다는 조건5를 건다면, 조건4에 의해 레드노드는 자식으로 레드노드를 가질 수 없게 되므로,

 

 A경로: 가장 길이가 긴 경우인 블랙-레드-블랙-레드-블랙 으로 블랙개수: 3, 높이: 4

 B경로: 가장 길이가 짧은 경우인 블랙-블랙-블랙 으로 블랙개수:3, 높이:2

 

이렇게 최악의 경우에도 최대 높이가 최저 높이의 2배를 초과하지 않게 되면서 적당히 균형을 이루도록 만드는 역할을 하는게 조건5이다.

2배를 초과하지 않는 이유는 블랙 사이사이 전부에 레드를 넣어줄 때 (경로 내 레드의 개수 = 경로 내 블랙의 개수 - 1)이라서 전체 높이는 2*블랙개수 - 2이고, 최저높이는 경로에 레드가 없는 경우로, 높이 = 블랙개수 - 1이 된다. 따라서 2배* (블랙개수 -  1) == 2*블랙개수 - 2 이므로 최악의 경우에도 2배를 초과하지 않는다.

(엄격한 균형을 유지하는 트리: AVL트리)

 

전제: 새로 추가될 노드의 색은 레드이다.

- 조건5를 만족하는 경우, 새 노드로 레드를 추가해도 경로의 블랙개수는 바뀌지 않기 때문에 여전히 조건5를 만족한다. 따라서 새 노드를 삽입한 후 우리가 체크해야 할 것은 조건4 밖에 없게 된다. 따라서 조건4를 만족하지 않는 경우에만 처리를 해주면 된다. 하지만 새 노드로 블랙을 넣는 경우, 특정 경로에 블랙이 추가되기 때문에 조건5를 무조건 위반하게 되면서 무조건 처리를 해주어야 한다. 따라서 새로 삽입되는 노드의 색을 레드로 한다.

 

삽입, 삭제: 추후 포스팅 예정

 

참고자료

위키피디아-트리

위키피디아-이진트리

위키피디아-자가균형 이진탐색트리

위키피디아-레드블랙트리

루트노드가 항상 블랙이어야 하는 이유

NIL노드의 필요성

이진탐색트리 시각화 사이트

레드블랙트리 시각화 사이트

chatgpt-관련 검색 기록(틀린 답변 존재)