99클럽 코테 스터디 15일차 TIL - 이미 방문한 곳도 다시 가는 DFS

문제 - 양과 늑대 문제링크

 

 

문제 설명

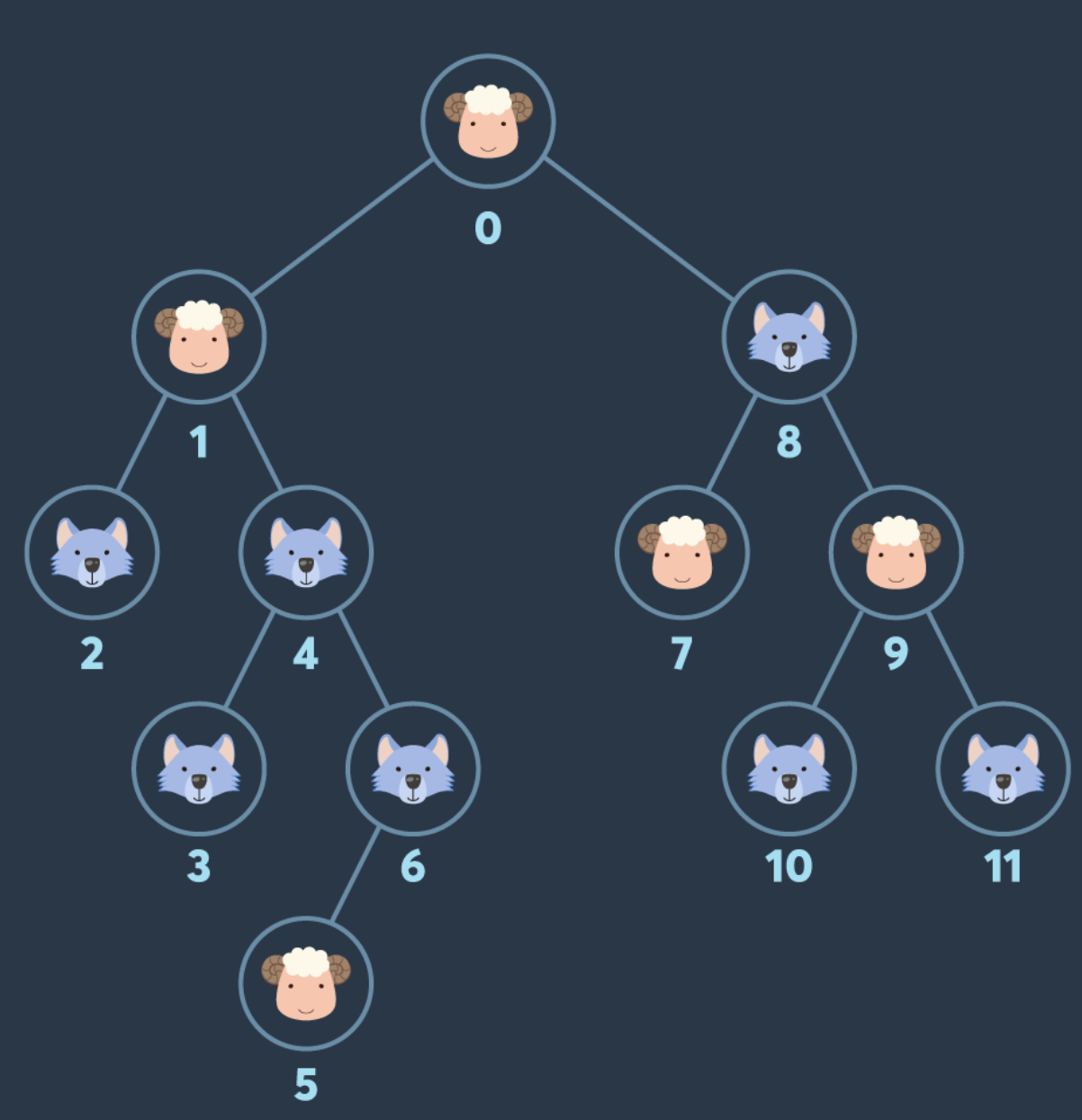
이렇게 생긴 이진트리가 주어집니다.

0번 루트노드부터 탐색을 시작하는데, 노드에 양이 있으면 양 누적 카운트를 + 1 해주고, 늑대가 있으면 늑대 누적 카운트를 + 1 해줍니다.

그런데 [양 누적 <= 늑대 누적]이 되는 순간 양은 늑대에게 다 잡아먹힙니다.

그래서 양이 늑대보다 많은 숫자를 유지하면서 최대한 양을 많이 모아야 합니다.

위 트리에서는 0->1 해서 일단 왼쪽 양을 구한 후, 1->0->8->7->8->9 이렇게 이동해서 우측 서브트리의 양까지 다 구할 수 있습니다. 

지금까지의 카운트는 양:4마리, 늑대:1마리이므로, 4번, 6번 늑대까지 방문해도 4대3으로 아직 괜찮습니다. 그래서 5번 양까지 구할 수 있습니다.

 

제한사항

트리의 노드 개수는 최대 17입니다.

 

풀이 과정

일단, 어떻게든 트리를 순회하면서 양과 늑대를 카운트해서 최대로 구할 수 있는 양을 구해야 합니다.

그리고, 한번 방문한 노드를 다시 방문할 수 있습니다. 다시 방문할 수는 있지만 특정 노드에 위치해 있을 때, 이미 해당 노드에서 같은 경로의 상태가 존재했었다면 방문하면 안됩니다. 중복이기 때문입니다. 예를 들어 설명하자면,

 

0->1->0 의 경로로는 이동할 수 있습니다. 현재 위치는 0번 노드이고, 0번 노드는 이번에 처음으로 0->1의 경로를 통해 도달했기 때문입니다. 

그러나, 0->1->0->1 의 경로로는 이동할 필요가 없습니다. 1은 맨 처음에 0->1에서 0을 방문한 상태였고, 이후 다시 0->1->0에서 1로 이동하게 되면 0->1의 경로로 1로 이동했을 때와 똑같은 상태이기 때문입니다.

 

똑같은 이유는 아직 방문하지 않은 노드에 방문하게 되면 해당 노드가 늑대인지, 양인지에 따라 카운트가 올라갑니다.

하지만, 이미 방문한 노드에 대해서는 카운트가 올라가지 않고 그저 건널 수 있는 다리 역할만을 수행합니다.

그래서 0->1과 0->1->0->1을 똑같은 상태라고 볼 수 있는 것입니다.

 

위 아이디어를 DFS와 비트마스킹을 이용해서 구현하면 다음과 같습니다.

"""
    지금 노드 개수가 17이기 때문에 비트마스킹 가능
    비트마스킹으로 방문체크해서 중복경로 차단.
    2^17 크기의 배열 필요 or set으로 체크
"""
def solution(info, edges):
    graph = [[] for _ in range(len(info))]
    for edge in edges:
        graph[edge[0]].append(edge[1])
        graph[edge[1]].append(edge[0])
    
    vis = [set() for _ in range(len(info))]
 
    maxSheeps = 0
    def dfs(node, curPath, sheeps, wolves):
        nonlocal maxSheeps
     
        maxSheeps = max(maxSheeps, len(sheeps))

        # 다음 노드로 가기
        for nxt in graph[node]:
            # 다음경로
            nxtPath = curPath | (1 << nxt)
            
            # 가 본 경로면 패스
            if nxtPath in vis[nxt]:
                continue

            # 안 가본 경로일 때,
            
            # 늑대인데 아직 갈 수 있으면 가기
            if info[nxt] == 1:
                if nxt in wolves:
                    vis[nxt].add(nxtPath)
                    dfs(nxt, nxtPath, sheeps, wolves)
                elif len(sheeps) > len(wolves) + 1:
                    vis[nxt].add(nxtPath)
                    wolves.add(nxt)
                    dfs(nxt, nxtPath, sheeps, wolves)
                    wolves.remove(nxt)
                
            # 양이면 가기
            if info[nxt] == 0:
                vis[nxt].add(nxtPath)
                if nxt in sheeps:
                    dfs(nxt, nxtPath, sheeps, wolves)
                else:
                    sheeps.add(nxt)
                    dfs(nxt, nxtPath, sheeps, wolves)
                    sheeps.remove(nxt)

    vis[0].add(1)
    dfs(0, 1, set([0]), set())
    
    return maxSheeps

우선 양방향 그래프로 바꾸기 위해 graph를 새로 만들어 할당하였고, 방문체크는 각 노드별 set을 생성한 후 경로를 집어넣으면서 중복체크에 사용하였습니다.

 

비트마스킹으로 방문체크 하는법은 다음과 같습니다.

만약 5개의 노드가 존재한다면, 00000 ~ 11111 이렇게 범위가 주어집니다. 여기서  n번째 자리수의 값이 0이면 n번째 노드는 아직 방문하지 않았다는 뜻입니다. 따라서 00000이면 모든 노드를 방문하지 않은 것이고, 11111이면 모든 노드를 방문했다는 뜻입니다.

 

그리고, 노드 각각에 대해 set이 필요한 이유는 00011 이어도 지금 위치가 첫번째 노드일 수도 있고, 두번째 노드일 수도 있는데, 위 두 케이스는 서로 다른 상태라고 봐야하기 때문입니다. 그래서 각각에 대해 set이 필요합니다.

 

| 비트 연산자를 이용해서 현재 노드에 방문했다는 정보를 추가할 수 있습니다.

 

이후에는 (시작노드, 현재경로, 양, 늑대) 인자를 받는 DFS 내부에서 다음 노드가 양인 경우와 늑대인 경우, 이미 방문한 노드인 경우와 아직 방문하지 않은 노드인 경우로 나누어 DFS를 호출하였습니다.

 

총평

지금은 노드 개수가 최대 17개라서 비트마스킹으로 풀어도 됐지만, 노드 개수가 더 커지면 다른 방법으로 풀어야 하는데 다른 방법도 찾아봐야겠습니다.

예전엔 못 풀었던 문제를 이제는 풀 수 있어서 성장한 것 같아 좋습니다.