99클럽 코테 스터디 16일차 TIL - 비슷한 문제가 생각날 때

문제1 - 부대 복귀 문제링크

문제 설명

양방향 그래프가 주어지고 출발지 노드들과 목적지가 주어질 때, 각 출발지에서 목적지 노드까지의 최단경로 거리를 구하는 문제입니다.

목적지에 도달할 수 없다면 -1입니다.

 

제약조건

노드n: 최대 10만개

간선roads: 최대 50만개

출발지sources: 최대 500개

 

풀이 과정

처음엔 그래프상에서 최단경로 길이를 구하는 문제라서 다익스트라를 사용해서 출발지 노드에서 목적지 노드까지의 최단경로거리를 구했습니다.

 

시행착오1(다익스트라, 실패)

import heapq

def solve(graph, dists, src, dest):
    q = []
    dists[src][src] = 0
    heapq.heappush(q, (0, src))

    while q:
        curDist, curPos = heapq.heappop(q)

        if curDist > dists[src][curPos]:
            continue

        for nxt in graph[curPos]:
            if dists[src][nxt] > curDist + 1:
                dists[src][nxt] = curDist + 1
                heapq.heappush(q, (dists[src][nxt], nxt))
    
    if dists[src][dest] == float('inf'):
        return -1

    return dists[src][dest]
    

    
def solution(n, roads, sources, destination):
    answer = []
    graph = [[] for _ in range(n + 1)]
    for road in roads:
        u, v = road
        graph[u].append(v)
        graph[v].append(u)

    dists = [[float('inf') for _ in range(n + 1)] for _ in range(n + 1)]

    for source in sources:
        if source == destination:
            answer.append(0)
        elif not graph[source]:
            answer.append(-1)
        else:
            res = solve(graph, dists, source, destination)
            answer.append(res)
        
    return answer

 

이후 제출한 결과 몇 개의 테스트케이스에 대해 시간초과가 발생했습니다.

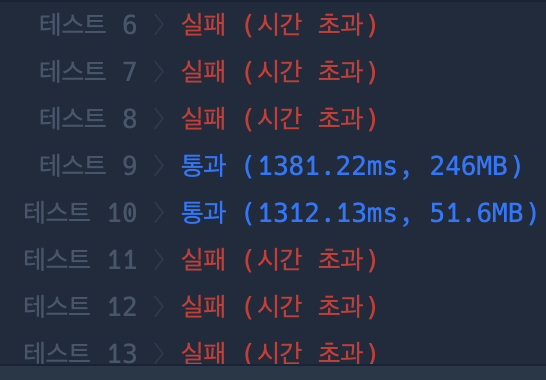
제 풀이의 시간복잡도를 계산해보면, O(len(source) * len(roads)*logn)입니다.

이는 최대 500 * 500000 * 16 = 40억회의 연산이 필요해서 사실상 시간초과가 발생할 수밖에 없습니다.

 

시행착오2(성공)

어떻게 하면 좀 더 빠를지 고민하다가, 문제를 뒤집어서 목적지에서 출발하여 인접 노드를 탐색하면서 최단거리를 갱신하는 방식으로 구현하였습니다.

from collections import deque

def solution(n, roads, sources, destination):
    answer = []
    
    q = deque()

    dists = [float('inf') for _ in range(n + 1)]

    graph = [[] for _ in range(n + 1)]
    for road in roads:
        graph[road[0]].append(road[1])
        graph[road[1]].append(road[0])

    for nxt in graph[destination]:
        q.append((nxt, 1))
        dists[nxt] = 1
    
    while q:
        curPos, cnts = q.popleft()

        if dists[curPos] != cnts:
            continue
        
        for nxt in graph[curPos]:
            if dists[nxt] > cnts + 1:
                dists[nxt] = cnts + 1
                q.append((nxt, dists[nxt]))
        
    for source in sources:
        if source == destination:
            answer.append(0)
        elif dists[source] == float('inf'):
            answer.append(-1)
        else:
            answer.append(dists[source])

    return answer

목적지에서 출발하여 다른 노드들까지의 최단거리만 구하면 되므로 한 번만 다익스트라 알고리즘을 수행하면 됩니다. 그래서 dists 배열을 1차원으로 구현할 수 있었습니다.

 

제출 결과

 

시행착오3(성공)

더 간단한 풀이는 없을까 고민하던 중, 어차피 간선의 가중치는 모두 1이라서 다익스트라를 굳이 사용할 필요가 없겠다라는 생각이 들었습니다. 그래서 일반적인 방문체크를 수행하는 BFS로 풀 수 있겠다고 생각했습니다.

from collections import deque
def solution(n, roads, sources, destination):
    answer = []
    graph = [[] for _ in range(n + 1)]
    for road in roads:
        graph[road[0]].append(road[1])
        graph[road[1]].append(road[0])

    q = deque()
    vis = set()
    q.append((destination, 0))
    vis.add(destination)
    dists = [-1 for _ in range(n + 1)]
    dists[destination] = 0

    while q:
        curPos, cnts = q.popleft()

        for nxt in graph[curPos]:
            if nxt in vis:
                continue
            vis.add(nxt)

            dists[nxt] = cnts + 1
            q.append((nxt, cnts + 1))
    
    for source in sources:
        answer.append(dists[source])

    return answer

목적지에서부터 시작하여 인접 노드를 BFS 탐색하며 최단거리를 구합니다. 이미 방문했던 노드라면 더 빠른 경로가 있었다는 뜻이기 때문에 다시 방문하지 않아도 됩니다.

 

제출 결과

 

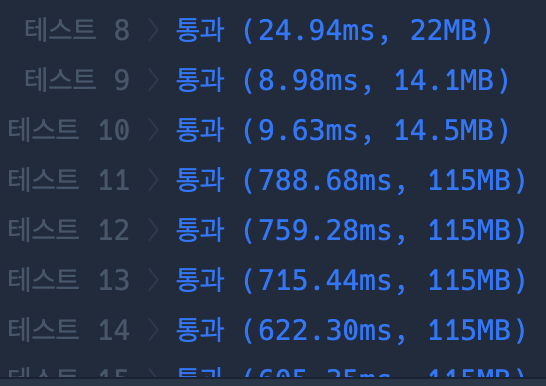
dist값을 비교하는 조건 대신 set을 이용해 방문체크를 하기 때문에 더 시간이 적게 걸렸습니다.

 

문제2 - 풍선 터뜨리기 문제링크

문제 설명

각자 고유한 숫자가 적힌 풍선이 일렬로 주어지는데, 인접한 두개의 풍선을 선택하고 그중 하나를 터뜨린 다음, 다시 풍선을 밀어서 빈 공간을 채웁니다.

이 과정을 풍선 하나가 남을 때까지 반복하는데, 풍선을 터뜨릴 때 규칙이 있습니다.

규칙: 일반적으로는 숫자가 더 큰 풍선을 터뜨리되, 단 한 번 숫자가 더 작은 풍선을 터뜨려도 됩니다.

우리가 구해야 할 것은, 모든 경우의 수를 다 체크해보았을 때 최후에 남을 풍선이 될 수 있는 풍선들을 모아 반환하는 것입니다.

 

풀이 과정

처음에 이 문제를 봤을 때는 DFS나 백트래킹같은 재귀함수 형태로 풀어야 할 것 같았습니다. 모든 경우를 다 체크해가면서 확인해야했기 때문입니다. 하지만, 단 한 번 숫자가 더 작은 풍선을 터뜨릴 수 있다는 규칙이 추가됨에 따라 어떻게 코드를 작성해야할지 어려움을 겪었습니다.

그래서 이 방법은 미뤄두고, 특정 풍선이 무조건 죽는 경우를 생각해보았습니다. 최악의 상황을 가정하여 풍선A와 A의 풍선이 계속 대결을 펼친다고 가정하겠습니다. 그럼 A보다 숫자가 큰 풍선은 모두 터질 것입니다. 마침내 A보다 작은 숫자 풍선들만 남을텐데, 이때 풍선A 양쪽에 풍선A보다 작은 숫자가 있다면 이 풍선은 살릴 수 없습니다.

이때 한쪽에만 더 작은 풍선이 있으면 1회용 스킬인 더 작은 숫자풍선 터뜨리기를 하면 되므로 살 수 있습니다. 더 작은 풍선이 한쪽에 2개 이상 있을지라도 그들끼리 터지는 과정속에서 1개만 남게될 것이고 이에 따라 한쪽에 작은 풍선이 1개만 있을 때만 고려해도 됩니다.

def solution(balloons):
    if len(balloons) <= 2:
        return len(balloons)
    
    answer = 2
    n = len(balloons)
    
    leftMin = [0 for _ in range(n)]
    rightMin = [0 for _ in range(n)]
    
    leftMin[0] = balloons[0]
    rightMin[n - 1] = balloons[n - 1]
    
    for i in range(1, n - 1):
        leftMin[i] = min(leftMin[i - 1], balloons[i])
        rightMin[n - i - 1] = min(rightMin[n - i], balloons[n - i - 1])
    
    for i in range(1, n - 1):
        answer += 1 if not (leftMin[i - 1] < balloons[i] and balloons[i] > rightMin[i + 1]) else 0
    
    return answer

 

제출결과

 

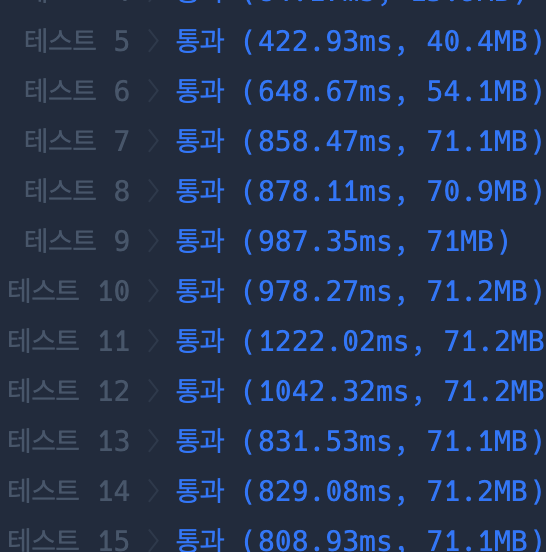
문제3 - 호텔 대실 문제링크

 

문제 설명

사람들이 호텔방을 특정 시간동안 사용하고 싶어합니다. 이때 방을 최소개수만 사용해서 사용 요청 리스트를 모두 처리하는 방 개수를 구하면 됩니다.

사용 요청은 [시작시간, 끝나는시간]형태로 주어지며, 끝난 후에는 10분간의 방 정리 시간이 필요해서 끝나고 10분 이후에 다시 해당 방에 손님을 받을 수 있습니다.

 

풀이 과정

우선, 시작시간이 빠르고, 만약 시작시간이 같다면 끝나는시간이 더 빠른 것이 앞에 오도록 정렬해줍니다.

정렬에 앞서, 시간값이 "시:분" 꼴의 문자열 형태로 주어졌기 때문에 해당 시간을 분으로 바꿔주는 toMinutes 함수를 만들어 숫자로 파싱한 후 정렬해주었습니다.

이후, 예약요청을 순회하면서, 현재 사용중인 방들의 끝나는 시간이 담겨 있는 최소힙에서 가장 빨리 끝나는 방을 뽑아봤을 때, 이 방에 들어갈 수 있다면 들어가고, 들어갈 수 없다면 나머지 확인하지 않은 방들은 전부 들어갈 수 없기 때문에 새로운 방을 하나 배정해줍니다.

import heapq

def toMinutes(s):
    temp = s.split(':')
    res = 60 * int(temp[0]) + int(temp[1])
    return res
    
def solution(book_time):
    # : 기준 파싱해서 튜플로 만들어 저장
    # 시작 시간기준 정렬
    # 순회하며 최소힙에 끝나는 시간 넣음
    # 최소힙에 아무것도 없거나 top 시간이 아직 안됐으면 방 하나 추가
    # 시간 됐으면 해당 요소 팝 시키고 추가
    
    for bt in book_time:
        for i in range(len(bt)):
            bt[i] = toMinutes(bt[i])
    
    book_time.sort()
    hq = []
    cnts = 0

    for bt in book_time:
        if not hq:
            cnts += 1
            heapq.heappush(hq, bt[1])
            continue
        
        if bt[0] < hq[0] + 10:
            cnts += 1
        else:
            heapq.heappop(hq)
        heapq.heappush(hq, bt[1])
            
            
    return cnts

 

제출결과

 

총평

까다로운 문제가 많았습니다. 풍선 문제는 예전에 리트코드에서 trapping rain water을 풀면서 leftMax, rightMax를 구해가며 풀었던 기억이 생각나서 풀 수 있었고, 호텔방 문제는 프로세스 스케쥴러나 철로 문제같은 스위핑 문제를 풀어보면서 정렬과 우선순위 큐의 활용에 익숙해져서 풀 수 있었습니다.